Question

Suzanne's salary grew from $40,000 in 2000 to $56,000 in 2021. during the same time period, Mike's salary grew form $38,000 to $53,000. Whose salary grew more in absolute change? In percentage change?

Answer 1

Answer: Mike's salary grew from $ 38,000 to $ 53,000.

Explanation:

Answer 2

Absolute change (AC) refers to the simple difference in the indicator over two periods. that is

`\begin{gathered} \text{AC (Suzanne)=56000-40000} \\ \text{AC (Suzanne)=16000} \end{gathered}`

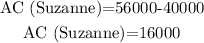
and, for Mike:

`\begin{gathered} \text{AC (Mike)=53000-3}8000 \\ \text{AC (Mike)=1}5000 \end{gathered}`

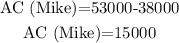
Whose salary grew more in absolute change? Suzanne's salary.

The relative change (RC) express the absolute change as a pencentage of the value of the indicator in the earlier period:

`RC=\frac{value\text{ 2nd period - value 1st period}}{\text{value 1st period}}*100`

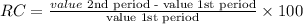
For Suzanne, we have

`\begin{gathered} RC(\text{Suzzane)}=(56000-40000)/(56000)\cdot100 \\ RC(\text{Suzzane)}=(16000)/(56000)\cdot100 \\ RC(\text{Suzzane)}=0.286\cdot100 \\ RC(\text{Suzzane)}=28.6 \end{gathered}`

and for Mike, we have

`\begin{gathered} RC(\text{Mike)}=(53000-28000)/(53000)\cdot100 \\ RC(\text{Mike)}=(15000)/(53000)\cdot100 \\ RC(\text{Mike)}=0.283\cdot100 \\ RC(\text{Mike)}=28.3 \end{gathered}`

In percentage change?​ For Suzanne is 28.6% and for Mike 28.3%