Question

13. Write the equation of a line with a slope of 2/3, which goes through the point (6,1). Equation:

Answer 1

Given in the question:

a.) The slope of the line (m) = 2/3

b.) Point passing through the line, x,y = 6,1

In writing the equation, let's first determine the y-intercept (b) by substituting the value of the slope and the point 6,1 in the slope-intercept formula.

`\text{ y=mx + b}`

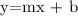
At m = 2/3 and x,y = 6,1

`\text{ y = mx + b }\rightarrow\text{ 1 = (}(2)/(3))(6)\text{ + b}`
`\text{ 1 = }(12)/(3)\text{ + b }\rightarrow\text{ 1 = 4 + b}`
`\text{ b = 1 - 4}`
`\text{ b = -3}`

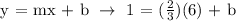
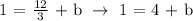
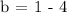
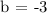
Let's now complete the equation by substituting the value of the slope (m) and the y-intercept (b) in the slope-intercept formula.

`\text{ y = mx }+\text{ b }\rightarrow\text{ y = (}(2)/(3))x\text{ + (-3)}`
`\text{ y = }(2)/(3)x\text{ - 3}`

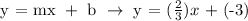
Therefore, the equation of the line is y=2x/3 - 3.