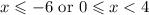For this problem, we need to solve the following inequality:
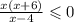
Since the expression is rational, it will be positive whenever both the numerator and denominator have the same signal, and it will be negative when their signals are different. Therefore we can evaluate these two expressions separately.
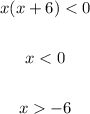
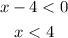
We can create the following table:
With this, the intervals are:
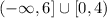
The algebraic intervals are: