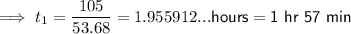Answer:
see below
Explanation:
Let t = time (in hours)
a) i) First 105 km of journey
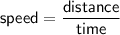
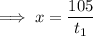
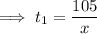
ii) Rest of journey
distance = 190 - 105 = 85 km
speed =
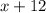 km/h
km/h
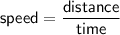
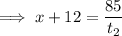
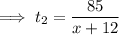
b) 3 hours 15 minutes = 3.25 hours
 total time =
total time =
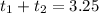
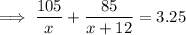
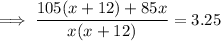
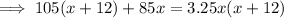
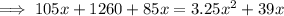
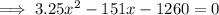
multiply by 4:
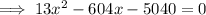
c)
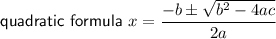
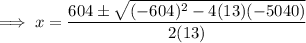
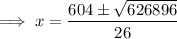
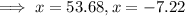
(to 2 decimal places)
d) time ≥ 0, therefore, x = 53.68 only
Substitute x = 53.68 into the expression for
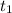 and solve for
and solve for
 :
: