In order to identify the transformations, first let's write the coordinates of each point:
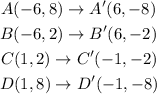
We can see that the coordinates of A, B, C and D changed the signals of x and y:
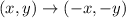
This means the transformation is a reflection about the origin.
Another way of transforming ABCD into A'B'C'D would be a reflection about the point (-2.5, 5), which is the center of ABCD, and then a translation of 5 units right and 10 units down.