Question

Consider a population that grows according to the recursive ruleLn+1 = Ln + 24,with an initial population Lo = 7.Find the next five terms in the sequence:L1 =L2 =L3 =L4L5 =

Answer 1

Given the recursive rule:

`L_(n+1)=L_n+24`

With an initial population of:

`L_o=7`

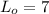
Let's determine the next five terms.

Since the first term is 7,

• For the L1, substitute 0 for n and solve:

`\begin{gathered} L_(0+1)=L_0+24 \\ \\ L_1=7+24 \\ \\ L_1=31 \end{gathered}`

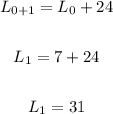
• For L2, substitute 1 for n and solve:

`\begin{gathered} L_(1+1)=L_1+24 \\ \\ L_2=31+24 \\ \\ L_2=55 \end{gathered}`

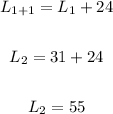
• For L3, substitute 2 for n and solve:

`\begin{gathered} L_(2+1)=L_2+24 \\ \\ L_3=55+24 \\ \\ L_3=79 \end{gathered}`

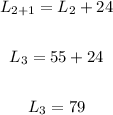
• For L4, substitute 3 for n and solve:

`\begin{gathered} L_(3+1)=L_3+24 \\ \\ L_4=79+24 \\ \\ L_4=103 \end{gathered}`

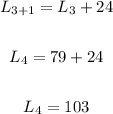
• For L5, substitute 4 for n and solve:

`\begin{gathered} L_(4+1)=L_4+24 \\ \\ L_5=103+24 \\ \\ L_5=127 \end{gathered}`

ANSWER:

• L1 = 31

,

• L2 = 55

,

• L3 = 79

,

• L4 = 103

,

• L5 = 127