84%
Step-by-step explanation
the concentration is given by
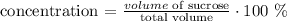
hence
Step 1
for the initial solution
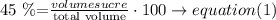
Step 2
after the evaporation

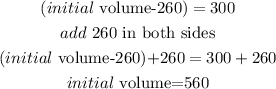
now, replace this value in step 1 to find the initial volume of sucrose
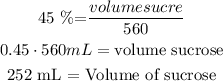
now, replace this value in eq(2)
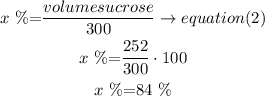
therefore, the answer is
84%
I hope this helps you