Question

A garden has an area of 336 ft2. Its length is 5 ft more than its width. What are the dimensions of the gardenand the length of the garden isThe width of the garden is(Simplify your answers.)

Answer 1

Given:

The area of the garden = 336 ft2.

The length is 5 ft more than its width.

Required:

To find the dimensions of the garden.

Step-by-step explanation:

Let the width of the garden = x ft

The length is 5 ft more than its width.

Now the length = x+5

The area of the garden = length x width

`\begin{gathered} 336=(x+5)\text{ }* x \\ 336=x^2+5x \\ x^2+5x-336=0 \end{gathered}`

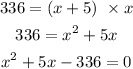
This is a quadratic equation we will solve it by using the middle term splitting method.

`\begin{gathered} x^2+21x-16x-336=0 \\ x(x+21)-16(x+21)=0 \\ (x+21)(x-16)=0 \\ x=-21,\text{ 16} \end{gathered}`

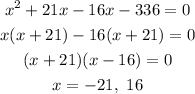
Since width can not be negative so we will take x=16.

Thus width = 16 ft

and length = 16+5 = 21 ft

Final answer:

Thus the length and width of the garden are 21 ft and 16 ft.