Answer: 144 minutes
Since the football field is 360 feet long and it takes 80 trips from end to end to mow the entire width of the football field, this would mean that the lawnmower would travel 80 x 360 in total:
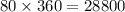
The lawnmower would have to travel 28,800 feet in total.
Now, since the lawnmower moves 200 feet per minute, we know that at the first minute, 200 feet have been mowed, and by the second minute, 400 feet have been mowed.
Putting this in a table:
We let x be the time in minutes while y is the distance mowed in feet.
With these, we can use the equation of the line to know how long would it take to mow the entire field.
The slope-intercept form of the equation of the line goes as:

Where:
m = slope
b = y-intercept
First, get the slope using the points (1, 200) and (2, 400)
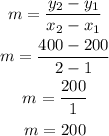
Then, we will solve for the y-intercept using the slope and the point (1, 200)
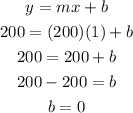
With these, our equation of the line would be:
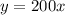
And since the total distance that needs to be mowed is 28, 800 feet, we will substitute y = 28, 800 and solve for x:
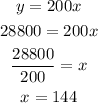
Therefore, it would take 144 minutes to complete 80 trips.