Question

Find the area of the shaded region.(Hint: Round to the nearest tenth)4 ftBlank 1:

Answer 1

We will determine the area of the shaded region as follows:

*First: We determine the area of the circle:

`A_c=\pi(4)^2\Rightarrow A_c=16\pi`

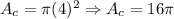
*Second: We determine the area of the hexagon:

**For this, we have that the internal angles of the sub triangles formed [in the hexagon] are:

`(360)/(6)=60`

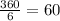
**Using this, we form two straight triangles and determine the value of the base of the triangle:

`6=b\sqrt[]{3}\Rightarrow b=\frac{6}{\sqrt[]{3}}`

**Now, we determine the area of the hexagon:

`A_h=(1)/(2)(\frac{6}{\sqrt[]{3}})(6)\Rightarrow A_h=6\sqrt[]{3}`

*Finally: We subtract the area of the hexagon from the area of the circle:

`A_s=16\pi-6\sqrt[]{3}\Rightarrow A_s=39.9`

So, the shaded area is approximately 39.9 square feet.