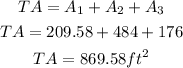The composite shape shown in the picture can be divided into three forms:
1) An equilateral triangle with side length a=22ft
The area of an equilateral triangle can be determined using the following formula:
![A_1=\frac{a^2\sqrt[]{3}}{4}](https://img.qammunity.org/2023/formulas/mathematics/college/9ssyp0yl6bx1v0xz4ho7f3n4pa27zonp5g.png)
Replace it with a=22ft
![\begin{gathered} A_1=\frac{22^2\sqrt[]{3}}{4} \\ A_1=\frac{484\sqrt[]{3}}{4} \\ A_1=209.58ft^2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i17lffkli8hxjl9nrhak3hn6a7b4f62rjz.png)
2) A square with side length a=22ft
The area of the square can be determined as the square of the side length:
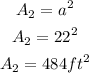
3) A triangle with height 22ft and base 16ft
The area of the triangle can be calculated as half the product of the base and the height:
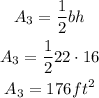
The total area of the composite shape is equal to the sum of the three areas: