Question

The number of bacteria in a refrigerated food product is given by N ( T ) = 29 T 2 − 160 T + 77 , 5 < T < 35 where T is the temperature of the food. When the food is removed from the refrigerator, the temperature is given by T ( t ) = 8 t + 1.2 , where t is the time in hours. Find the composite function N ( T ( t ) ) : N ( T ( t ) ) = Find the number of bacteria after 4.1 hours. Give your answer accurate to the nearest whole value. bacteria

Answer 1

Given:

The number of bacteria in a refrigerated food product is given by:

`N(T)=29T^2-160T+77`

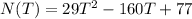
where (T) is the temperature of the food.

When the food is removed from the refrigerator, the temperature is given by:

`T(t)=8t+1.2`

where (t) is the time in hours.

We will find the composite function N(T(t))

So, we will substitute the function (T) into the function (N):

`N(T(t))=29(8t+1.2)^2-160(8t+1.2)+77`

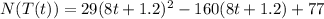
Expand the function then simplify it:

`\begin{gathered} N(T(t))=29(64t^2+19.2t+1.44)-160(8t+1.2)+77 \\ N(T(t))=1856t^2+556.8t+41.76-1280t-192+77 \\ \\ N(T(t))=1856t^2-723.2t-73.24 \end{gathered}`

So, the composite function will be:

`N(T(t))=1,856t^(2)-723.2t-73.24`

Now, we will find the number of bacteria after 4.1 hours.

So, substitute t = 4.1 into the composite function

`\begin{gathered} N(T(t)=1856(4.1)^2-723.2(4.1)-73.24 \\ N(T(t))=28161 \end{gathered}`

So, the answer will be:

The number of bacteria after 4.1 hours = 28161 bacteria