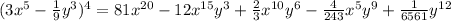a)
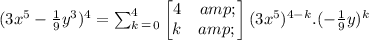
b)
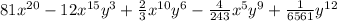
STEP - BY - STEP EXPLANATION
What to find?
• The sum in summation notation that he used to express the expansion.
,
• The simplified term of the expression.
Given:
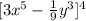
a)
The binomial theorem formula is given below:
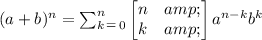
To obtain the sum in summation that Harold used, simply substitute a=3x⁵ ,
b=-1/9y³ and n=4 into the above formula.
That is;
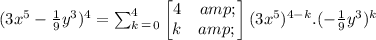
b)
We can now proceed to expand the above.
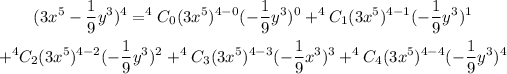
Simplify the above.
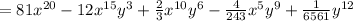
Hence, the simplified form of the expression is given below: