Question

How do I solve for the volume of thsi cone

Answer 1

Given the cone as shown below

The volume of a cone is evaluated as

`\begin{gathered} \text{Volume = }(1)/(3)^{}*\pi\text{ }* r^2* h \\ \text{where} \\ r\text{ is the radius of the circular base of the cone} \\ h\text{ is the height of the cone} \end{gathered}`

From the above figure,

radius of the circular base = YZ

height of the cone = XY

To evaluate the radius and height of the cone:

XYZ is a right-angled triangle.

Thus, using trigonometric ratios, we can evaluate XY and YZ.

height of the cone:

`\begin{gathered} \sin \text{ 54 =}(XY)/(XZ) \\ \Rightarrow\sin \text{ 54 = }(h)/(15) \\ h=15*\sin \text{ 54 = 15 }*0.8090 \\ \Rightarrow h=12.14\text{ cm} \end{gathered}`

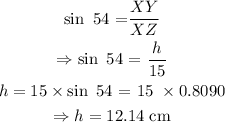
radius of the cone: