Question

The weights of certain machine components are normally distributed with a mean of 8.34 g and a standard deviation of 0.09 g. Find the 97th percentile.

Answer 1

To answer this question, we need to use the standard normal distribution to find the 97th percentile. We need to normalize the given values, and then equates the equation to that value when the probability is equal to 97%.

Then, we have:

`z=(x-\mu)/(\sigma)`

We have that the raw value is the one we need to find. Then, we need to find, using the standard normal distribution table, to find the z-score for a probability of 97%. Then, we have that, for this value, the corresponding z-score is, approximately, z = 1.88. Thus, we have:

`1.88=(x-8.34)/(0.09)\Rightarrow1.88\cdot0.09=x-8.34`

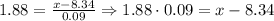
Then, we have

`1.88\cdot0.09+8.34=x\Rightarrow x=8.5092\approx8.51`

Therefore, the 97th percentile is, approximately, equal to x = 8.51 (rounding the value to the nearest hundredth) or x = 8.5092.