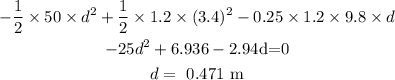Given that the mass of the object is m = 1.2 kg
The coefficient of kinetic friction is given as
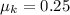
The speed of the object is
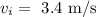
The force constant is
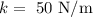
We have to find the compression, d.
According to the conservation of energy
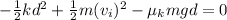
Here, g = 9.8 m/s^2 is the acceleration due to gravity.
Substituting the values, the compression will be