The given function is:
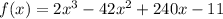
It is required to find the x values for which the graph has a horizontal tangent line.
Recall that horizontal lines have a slope of 0.
Recall also that the derivative of a function at a point is the same as the slope of the tangent line at that point.
Hence, to find the x values at which the graph of the function has horizontal tangent lines, find the derivative of the function and equate it to zero.
Find the derivative of the function:
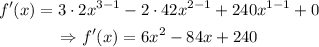
Equate the derivative to zero and solve the resulting equation for x:

Hence, the x-values are x=4 and x=10.
The required x values are 4 and 10.