Question

IF AQRS = AMNP, OR = 11, QS = 15, MP = 2x + 1, mZS = 84, mZR = 32', and mZM = (17y - 4),find the values of x and y.

Answer 1

Let's make a drawing first

We have enough information to find the remaing angle in triangle QRS. The interior angles of a triangle add up 180º. So:

`180º=m\angle Q+84º+32º\Rightarrow m\angle Q=180º-84º-32º=64º`

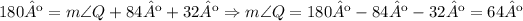
Since both triangles are approximately the same, the measure of M is the same than the measure of Q:

`m\angle M\approx m\angle Q`
`17y-4=64º`

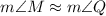
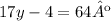
Now we just clear y:

`y=(64+4)/(17)=4º`

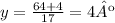
y = 4º

For the same reason, segments QS and MP are approximately the same too:

`15\approx2x+1`

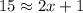
Then we clear x:

`x=(15-1)/(2)=7º`

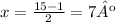
x = 7º