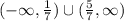Question

I would like to know how i got this answer

Answer 1

Given:

`3-2\lvert7x-3\rvert<-1`

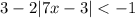
Solution:

First, we need to transfer 3 to the other side.

`\begin{gathered} 3-2\lvert7x-3\rvert<-1 \\ -2\lvert7x-3\rvert<-1-3 \\ -2\lvert7x-3\rvert<-4 \end{gathered}`

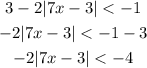
Then, we will divide both sides with -2 to isolate the terms with absolute value.

`\begin{gathered} -2\lvert7x-3\rvert<-4 \\ (-2\lvert7x-3\rvert)/(-2)<(-4)/(-2) \\ \lvert7x-3\rvert>2 \end{gathered}`

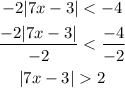
Now, in dealing with absolute value, we will set it's limits.

`\begin{gathered} \lvert7x-3\rvert>2 \\ \text{absolu}te\text{ value can also be written as:} \\ -2>7x-3>2 \end{gathered}`

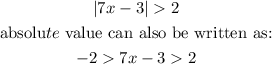
Let's equate the inequalities separately.

`\begin{gathered} 7x-3>2 \\ 7x>2+3 \\ 7x>5 \\ (7x)/(7)>(5)/(7) \\ x>(5)/(7) \end{gathered}`

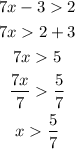
For the other equation:

`\begin{gathered} 7x-3<-2 \\ 7x<-2+3 \\ 7x<1 \\ (7x)/(7)<(1)/(7) \\ x<(1)/(7) \end{gathered}`

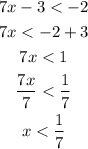
Therefore, we will have x is less than 1/7 and greater than 5/7.

ANSWER:

`(-\infty,(1)/(7))\cup((5)/(7),\infty)`