ANSWER
The probability of picking 2 almond cookies without replacing it is 1/5
Step-by-step explanation
Given that
The total number of cookies in the box is 6
The number of chocolate cookie is 1
The number of almond cookies is 3
The number of butter cookies is 2
Probability is defined as likelihood of an event to happen
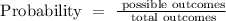
Recall, that the condition given is without replacement
So, probability of picking 1 almond cookie first is
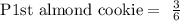
Since, the first almond cookie picked was not replaced, then, the total number of cookies in the box will be 5 and also, the number of almond cookies will be 2
hence, the probability of picking the second almond is

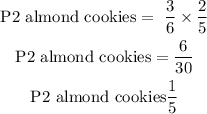
Therefore, the probability of picking 2 almond cookies without replacing it is 1/5