Question

find the missing side of each triangle.Leave your answers in simplest radical form.A 6cmB√78cmC√14cmD√10cmE√114cm

Answer 1

In order to find the length of the third side, we can use the Pythagoras theorem.

The Pythagoras theorem can be used in right triangles, and it is a relation between the hypotenuse (h) and the two legs of the triangle (a and b):

`h^2=a^2+b^2^{}`

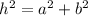
In the triangle given, the hypotenuse is 8 cm, and the legs are 5√2 cm and x.

So using the Pythagoras theorem, we have that:

`\begin{gathered} 8^2=(5\sqrt[]{2})^2+x^2 \\ 64=25\cdot2+x^2 \\ 64=50+x^2 \\ x^2=64-50 \\ x^2=14 \\ x=\sqrt[]{14}^{} \end{gathered}`

So the value of x is √14 cm, therefore the correct option is C.