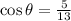In a rigth triangle:
θ
The cosine ratio is:
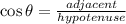
In the triangle given, we don't know the length of the adjacent leg to θ. We can find it using the pythagorean theorem:
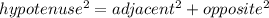
In this case:
hypotenuse = 13
opposite = 12
Then:
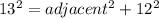
And solve:
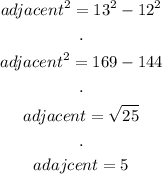
Now, we can find the cosine ratio: