Question

What are the equations of lines m and q?n(296)(4,4)m(1,-1)The equation of line mis

Answer 1

Lines n and q are parallel.

Line m is perpendicular to n and q.

To solve this exercise you have to keep the following rules in mind:

• The slope of two parallel lines are equal.

,

• The slope of the perpendicular line is the negative inverse of the original line.

So, considering that we have the most information from line n, the first step is to find its equation:

Slope:

Using the fiven points (4,4) and (1,-1) apply the following formula to determine the slope:

`(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1)=(4-(-1))/(4-1)=(5)/(3)`

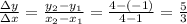
The slope for line n is 5/3

Next is to find its equation using one of the points, for example point (4,4)

For this use the point slope form:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-4=(5)/(3)(x-4) \\ y-4=(5)/(3)x-(20)/(3) \\ y=(5)/(3)x-(20)/(3)+4 \\ y=(5)/(3)x-(8)/(3) \end{gathered}`

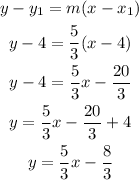
The equation for line n is y=5/3x-8/3

Line q

This line is parallel to line n, which means that they have the same slope. Then the slope for q is 5/3.

This line crosses the point (2,6), using this pot and the point slope form you can determine the equation for q:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-6=(5)/(3)(x-2) \\ y-6=(5)/(3)x-(10)/(3) \\ y=(5)/(3)x-(10)/(3)+6 \\ y=(5)/(3)x+(8)/(3) \end{gathered}`

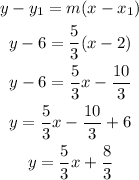
The equation for line q is y=5/3x+8/3

Line m

For line m we know that it is perpendicular to lines q and n, so it slope will be the inverse negative of the slope for q and n.

Slope:

If the slope for n is 5/3 then the negative inverse will be: -3/5

m also intersects point (2,6), so using this point and the point slope form you can determine the equation for line m as:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-6=-(3)/(5)(x-2) \\ y-6=-(3)/(5)x+(6)/(5) \\ y=-(3)/(5)x+(6)/(5)+6 \\ y=-(3)/(5)x+(36)/(5) \end{gathered}`

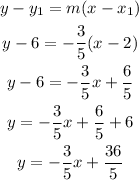
The equation for line m is y=-3/5x+36/5