Question

(A)Which figures have a volume greater than 600 cubic inches (b)How many times greater is the volume of the sphere than the volume of cone 1. Round your answer to the nearest tenth. "

Answer 1

(A)Cylinder 2 and the sphere

(B)4.8

Step-by-step explanation:

`\begin{gathered} \text{Volume of a cylinder =}\pi r^2h \\ \text{Volume of a cone=}(1)/(3)\pi r^2h \\ \text{Volume of a sphere=}(4)/(3)\pi r^3 \end{gathered}`

Cylinder 1

`\begin{gathered} \text{Volume}=\pi*6^2*5 \\ \approx565\text{ cubic inches} \end{gathered}`

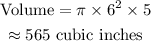
Cylinder 2

`\begin{gathered} \text{Volume}=\pi*6^2*15 \\ \approx1696\text{ cubic inches} \end{gathered}`

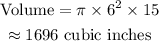
Cone 1

`\begin{gathered} \text{Volume}=(1)/(3)*\pi*6^2*5 \\ \approx188\text{ cubic inches} \end{gathered}`

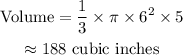
Cone 2

`\begin{gathered} \text{Volume}=(1)/(3)*\pi*6^2*15 \\ \approx565\text{ cubic inches} \end{gathered}`

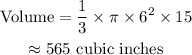
Sphere

`\begin{gathered} \text{Volume}=(4)/(3)*\pi*6^3 \\ \approx905\text{ cubic inches} \end{gathered}`

Therefore: Cylinder 2 and the sphere have a volume greater than 600 cubic inches ​.

Part B

`\begin{gathered} \text{Difference}=\frac{Volume\text{ of sphere}}{\text{Volume of cone 1}} \\ =((4)/(3)*\pi*6^3)/((1)/(3)*\pi*6^2*5) \\ =288\pi/60\pi \\ =4.8 \end{gathered}`

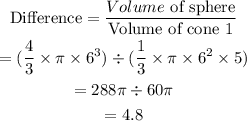
The volume of the sphere is 4.8 times greater than the volume of cone 1.