Question

Answer the following questions for the function f(x) = x * sqrt(x ^ 2 + 4) defined on the interval |-4<= x<=6 .

Answer 1

To define the concavity we must find the derivatives of the function:

`\begin{gathered} f(x)=x√(x^2+4) \\ f^(\prime)(x)=(x^(\prime))(√(x^2+4))+(x)(√(x^2+4))^(\prime) \\ f^(\prime)(x)=1(√(x^2+4))+x((x)/(√(x^2+4))) \end{gathered}`
`\begin{gathered} f^(\prime)(x)=(√(x^2+4))+((x^2)/(√(x^2+4))) \\ f^(\prime)(x)=(x^(2))/(x^(2)+4)+(√(x^2+4)√(x^2+4))/(√(x^2+4)) \\ f^(\prime)(x)=(x^2+(√(x^2+4))^2)/(√(x^2+4)) \\ f^(\prime)(x)=(x^2+x^2+4)/(√(x^2+4)) \\ f^(\prime)(x)=(2x^2+4)/(√(x^2+4)) \end{gathered}`

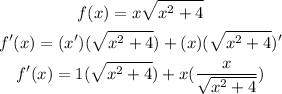
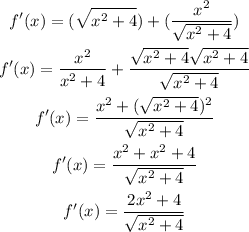
Now, we will continue finding the second derivative:

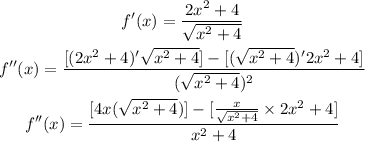
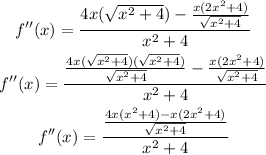
`\begin{gathered} f^(\prime)(x)=(2x^2+4)/(√(x^2+4)) \\ f^(\prime\prime)(x)=\frac{{}\lbrack(2x^2+4)^(\prime)√(x^2+4)\rbrack-\lbrack(√(x^2+4))^(\prime)2x^2+4\rbrack}{(√(x^2+4))^2} \\ f^(\prime\prime)(x)=(\lbrack4x(√(x^2+4))\rbrack-\lbrack(x)/(√(x^2+4))*2x^2+4\rbrack)/(x^2+4) \end{gathered}`
`\begin{gathered} f^(\prime\prime)(x)=(4x(√(x^2+4))-(x(2x^2+4))/(√(x^2+4)))/(x^2+4) \\ f^(\prime)^(\prime)(x)=((4x(√(x^2+4))(√(x^2+4)))/(√(x^2+4))-(x(2x^2+4))/(√(x^2+4)))/(x^2+4) \\ f^(\prime\prime)(x)=((4x(x^2+4)-x(2x^2+4))/(√(x^2+4)))/(x^2+4) \end{gathered}`

Now we will find the roots of the first and second derivatives so that we will have the critical points:

Due to in the first derivative there is no solution for y=0 in the reals, we have no first-order critical points.

For the second derivate:

`f^(\prime\prime)(x)=(2x^3+12x)/((x^2+4)(x^2+4))=0`

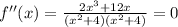
As we can see, the second derivative becomes zero when x=0, being the only critical point of second order.

We proceed to replace x=0 in the function f(x), and obtain as a result f(0)=0, being (0,0) the coordinate of the critical point.

Taking into account the given interval and the value of the second order critical point obtained, we have two new intervals:

`\begin{gathered} for\text{ }x=-1 \\ f´´(x)=-\frac{14\sqrt[\placeholder{⬚}]{5}}{25} \\ for\text{ }x=1 \\ f´´(x)=(14√(5))/(25) \end{gathered}`

By the criterion of the second derivative, we can deduce that the function is concave downward in the interval [-4,0) because it gave negative and is concave upward in (0,6) because it gave positive.

So the answers are:

F(x) is concave down on the interval x=-4 to x=0

F(x) is concave up on the interval x=0 to x=6

The inflection point for this function is at x= 0

The minimum occurs at x=-4

The maximum occurs at x=6