Given:
Area of the rectangle = 40 square units
The length is 6 units greater than the width.
Required:
To find the dimensions of the rectangle.
Step-by-step explanation:
Let the width of the rectangle = x unit
Since the length is 6 units greater than the width.
So length = x+6 unit
Now the area of the rectangle = length x width
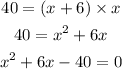
This equation is a quadratic equation, we will solve it by using the middle term splitting method.
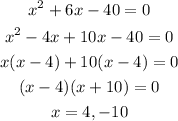
Since dimensions can not be negative so we will take the positive value.
width = 4 unit
length = 4+6 = 10 unit
Final answer:
The dimensions of the rectangle are 4 and 10.
Thus option (B) is the correct answer.