Given the function
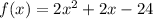
To find the x and y intersects of the parabola you have to do as follows:
y-intercept
This is the value of f(x) when x=0, to find it replace the value in the formula:
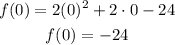
The y-intercept of the parabola is (0,-24)
Vertex
Calculate the x coordinate using the following formula:
For

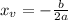
For this function:
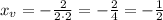
Using this value of x imput it in the formula to reach the value of the y-coordinate of the vertex:

The vertex is (-1/2,-49/2)
Using these two points you can draw the function:
Using the graph you can determine the x-intercepts of the function, these are (-4,0) and (3,0)