Question

At the end of a snow storm, Zoey saw there was a lot of snow on her front lawn. The temperature increased and the snow began to melt at a steady rate. Let SS represent the depth of snow on Zoey's lawn, in inches, tt hours after the snow stopped falling. The table below has select values showing the linear relationship between tt and S.S. Determine how many hours it would take for the depth of snow to reach 3.75 inches.

Answer 1

Let's find the equation of the line relating "t" and "S".

The formula we are going to use is:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

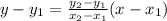
Where

(x1, y1) and (x2, y2) are two points through which the line goes through

Note: We are going to use "t" and "S" in place of "x" and "y" later

Let's take 2 points from the table of values:

`\begin{gathered} (x_1,y_1)=(2,9) \\ \text{and} \\ (x_2,y_2)=(5,4.5) \\ \end{gathered}`

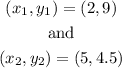
Now, let's substitute these values and find the equation of the line. The steps are outlined below:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-9=(4.5-9)/(5-2)(x-2) \\ y-9=(-4.5)/(3)(x-2) \\ y-9=-1.5(x-2) \\ y-9=-1.5x+3 \\ y=-1.5x+3+9 \\ y=-1.5x+12 \end{gathered}`

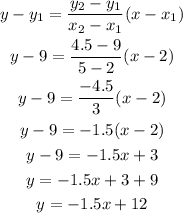
In terms of "t" and "S", we can write >>>

`S=-1.5t+12`

We want the time (t) it will take for depth (S) of snow to be 3.75 inches.

So, we put "3.75" into S and solve for "t". Shown below:

`\begin{gathered} S=-1.5t+12 \\ 3.75=-1.5t+12 \\ 1.5t=12-3.75 \\ 1.5t=8.25 \\ t=(8.25)/(1.5) \\ t=5.5 \end{gathered}`Answer5.5 hours