Question

waiting times (in minutes) of customers in a bank where all customers enter a single waiting line and a bank where customers wait in individual lines at three different teller windows are listed below. Find the mean and median for each of the two samples, then compare the two sets of results.

Answer 1

The mean of a set of values is the average value and it can be found by adding up all the numbers and dividing the result by the total number of values, and the median is the middle number of the set and it can be found by ordering the list from smallest to largest and finding the number in the middle.

The formula for mean is:

`\bar{x}=(\sum_^x)/(n)`

For the first data set, the mean is:

`\begin{gathered} \bar{x}=(6.3+6.5+6.6+6.7+7.0+7.3+7.5+7.8+7.8+7.8)/(10) \\ \\ \bar{x}=(71.3)/(10)=7.13 \end{gathered}`

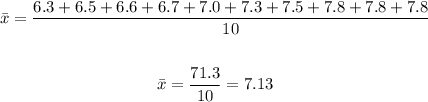
And for the second data set, the mean is:

`\begin{gathered} \bar{x}=(4.0+5.2+5.9+6.2+6.5+7.8+7.8+8.6+9.2+10.1)/(10) \\ \\ \bar{x}=(71.3)/(10)=7.13 \end{gathered}`

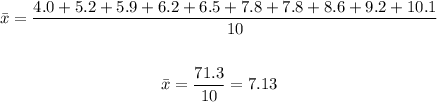
As we can observe, the mean for the two lists is equal. Now, let's find the median.

As we have a total number of data that is an even number, then we need to apply the following formula:

`M=(((n)/(2))^(th)term+((n)/(2)+1)^(th)term)/(2)`

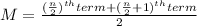
For the first data set, the median is:

`M=(7.0+7.3)/(2)=(14.3)/(2)=7.15`

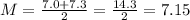
And for the second data set, the median is:

`M=(6.5+7.8)/(2)=(14.3)/(2)=7.15`

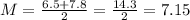
Now, the median is equal too.

Finally, if we analyze the data set, we can see a difference between the two data sets that is not apparent from a comparison of the measures of the mean and median.

We can observe, that the times for customers in individual lines are much more varied than the times for customers in a single line, then the answer is option A.