In general, a geometric sequence is given by the formula.
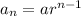
Then, in our case,
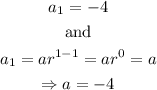
And, since the second term is 12,
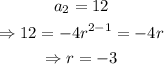
Thus, the formula is
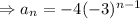
However, there is a mistake in the sequence given in the question.
Notice that if n=4, none of the options gives us a_4=144.
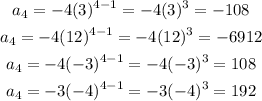
The third option gives us correctly the first three terms of the sequence. The answer is the third option (top to bottom)