Hello there. To solve this question, we have to remember some properties about derivatives.
Given the following expression:

Whereas x, z and θ are functions of the time, t.
We know that
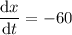
We want to determine the value for
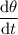
When z = 2, θ = π/6 and

For this, we have to use implicit differentiation.
Since the variables are function of time, we differentiate both sides of the equation with respect to the time t.

Knowing the Chain Rule:
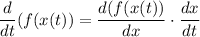
And the derivative of the sine and quotient rules, we get

Plugging the values, we get
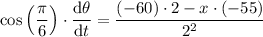
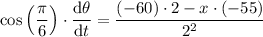
Of course, to find the value of x, we use the values for the angle and z in the former expression:
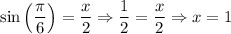
Therefore we get
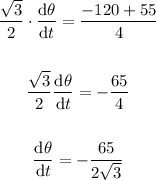
Using a calculator, we find a number accurate to two decimal places:
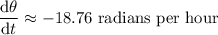
or rph.