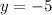Firstly we need to find the slope of the plotted line;
we will pick two points on the line and apply the slope formula;

Let's select points;

Substituting into the formula, we have;
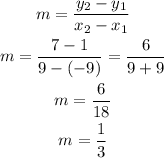
Since we have the slope and a point (3,-4) on the new line we can use the point slope formula to find the equation of the line.

Substituting the point and the slope,we have;
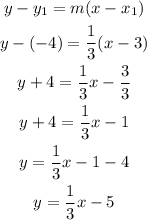
From the equation, the y intercept is the point where x = 0.
y intercept is;
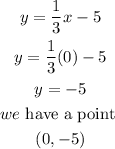
So we have two points on the new line.
Let us proceed to locate the two points and join to produce the new line;
Above is a graph of a line parallel to the line in problem 1, with the same slope and passes through point (3,-4).
The slope intercept equation of the line is;
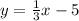
The point slope form of the equation is;
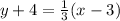
The slope of the line is;
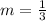
y-intercept is;