Question

Solve the system of equations 7x + 2y = 4 and -5x – 3y = 5 by combining theequations.

Answer 1

We have two equations to solve simultenously

7x + 2y = 4-------------1

-5x - 3y = 5-------------2

make x subject of the formular in both equation 1 and 2

In equation 1

7x + 2y = 4

7x = 4 - 2y

`x\text{ = }\frac{4\text{ -2y}}{7}`

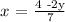
In equation 2

-5x -3y = 5

-5x = 5 +3y

`x\text{ = }(5+3y)/(-5)\text{ = -}\frac{(5\text{ +3y)}}{5}`

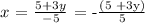
Thus , the x in equation 1 is equvalent to x in equation 2

Hence, we will equate their values

`\begin{gathered} (4-2y)/(7)\text{ = -}((5+3y))/(5) \\ \text{cross multiply} \\ 5\text{ }*\text{ (4-2y) = 7 }*(-5-3y) \\ \text{removing bracket} \\ 5\text{ }*4\text{ - 5}*2y\text{ = 7}*-5\text{ -7}*3y \end{gathered}`
`\begin{gathered} \text{ 20 -10y = -35 -21y} \\ \text{collect like terms} \\ -10y\text{ +21y = -35 -20} \\ 11y\text{ = -55} \\ \text{divide both side by 11} \\ (11y)/(11)=(-55)/(11) \\ y\text{ = -5} \end{gathered}`

substitute y = -5 in equation 1 to obtain x

7x +2y = 4

`\begin{gathered} 7x\text{ + 2 (-5) = 4} \\ 7x\text{ - 10 = 4} \\ 7x\text{ = 4+10} \\ 7x\text{ =14} \\ \text{divide both side by 7} \\ (7x)/(7)=(14)/(7) \\ x\text{ = 2} \end{gathered}`

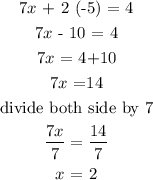
The solutions are x= 2 and y = -5