We are asked to determine the current input for a transformer. To do that we will use the following formula:
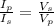
Where:
![\begin{gathered} I_p=\text{ primary or input current} \\ I_s=\text{ secondary or output current} \\ V_s=\text{ secondary voltage} \\ V_p=\text{ primary voltage} \end{gathered}]()
Now, we solve for the primary current by multiplying both sides by the secondary current:
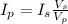
Now, we plug in the values:
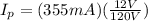
Solving the operations:
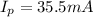
Therefore, the output current is 35.5 mA.
Part b. To determine the power input we use the following formula:
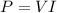
Since we want to determine the input power we use the value of primary current and voltage:
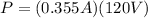
Solving the operations:
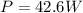
Therefore, the power is 42.6 Watts.