Question

1. The spinner shown has six equal-size sections and is spun twice. What is the probability that the product of the number spun is 12?2. A number from 0 to 9 is randomly selected and then a letter from A to D is randomly selected. What is the probability that the number 3 and a consonant are selected?

Answer 1

PART 1.

Out of the 6 numbers of the board, there are 2 pairs whose product is 12: 6 and 2, and 4 and 3.

Notice that you could spin, for instance, a 6 first and then a 2. Or you could also spin a 2 first and then a 6. This tells us that each pair of numbers can be spun in two different ways. This gives us a total of 4 possible combinations whose product is 12:

`\begin{gathered} (6,2) \\ (2,6) \\ (4,3) \\ (3,4) \end{gathered}`

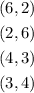
Now, let's calculate the number of possible combinations. Notice that, for example, you can spin a 1 and then a 1, 2, 3, 4, 5 or 6. This will give us 6 possible combinations for number 1:

`\begin{gathered} (1,1) \\ (1,2) \\ (1,3) \\ (1,4) \\ (1,5) \\ (1,6) \end{gathered}`

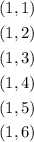
This will also happen for each of the 6 numbers on the board. If each number gives us 6 combinations, and there are 6 numbers, the total number of combinations will be:

`6\cdot6=36`

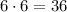
Now, we take the number of favorable outcomes (the pairs whose product is 12) and divide it by the total number of outcomes:

`(4)/(36)\rightarrow(1)/(9)`

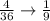
This way, we can conclude that the probability that the product of the numbers spun is 12 is 1/9.

PART 2.

Number 3 is one of the 10 numbers given (0,1,2,3,4,5,6,7,8,9). This way, the probability of choosing number 3 is:

`(1)/(10)`

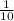
Now, out of all the 4 letters given (A,B,C,D), 3 are consonants. This way, the probability of choosing a consonant is:

`(3)/(4)`

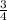
This way, the probability of chosing number 3 and a consonant is:

`(1)/(10)\cdot(3)/(4)=(3)/(40)_{}`

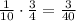
This way, we can conclude that the probability that the number 3 and a consonant are selected is 3/40