Question

A mine of mass 190 kg in a volume of 1.150 m³ is shown in the figure. If the tension in the chain is 5.6×10^3 N. What is the density of the fluid that the mine is in?

Answer 1

661.61 kg/m³

Step-by-step explanation

Given:

• The mass of the mine, m = 190 kg

,

• The volume of the mine, V = 1.150 m³

,

• The tension in the chain, T = 5.6x10³ N = 5600 N

Find:

• The density of the fluid, ρ

Let's draw a free-body diagram of this situation first,

If the forces are in equilibrium,

`F_b-T-F_g=0`

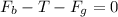
The buoyant force is given by the equation,

`F_b=\rho gV`

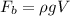
Where ρ is the density of the fluid, and V is the submerged volume - in this case, the volume of the mine. We know the magnitude of the tension in the chain and the weight of the mine is,

`F_g=mg`

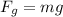
Replace in the first equation,

`\rho gV-T-mg=0`

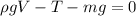
Solving for ρ,

`\rho=(T+mg)/(gV)`

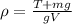
Replace with the known values and use g = 9.81 m/s²,

`\rho=(5600N+190kg\cdot9.81m/s^2)/(9.81m/s^2\cdot1.150m^3)\approx661.61kg/m^3`

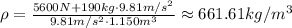
Hence, the density of the fluid the mine is in is 661.61 kg/m³.