1) In order to find the proportion of bulbs that are expected to last within 2 standard deviations of the mean, we need to find the value in the z-table that corresponds to z = -2 and z = 2, then find the difference of these values.
For z = -2, we have 0.0228, and for z = 2 we have 0.9772, so the difference is:
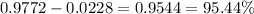
2) First let's find the values of z that corresponds to that interval:
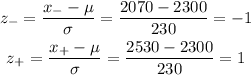
Looking at the z-table for z = -1 and z = 1, we have 0.1587 and 0.8413, so the probability of the interval is:
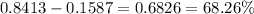
3) To find how many will last longer than 2530, we know that this value corresponds to z = 1, so the value in the table is 0.8413.
The percentage of bulbs that will last longer than this is:
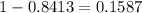
And the number of bulbs would be:
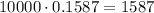
Rounding to the nearest whole number, we have 1587 bulbs.
4) First let's find the z-score for 1840:
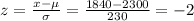
Looking at the table for z = -2, we have 0.0228, so the number of bulbs would be:
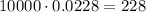
So 228 bulbs would last less than 1840 days.
5) Finding the z-score for this interval, we have:
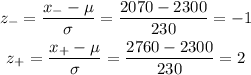
The value for z = -1 is 0.1587, and the value for z = 2 is 0.9772, so we have:
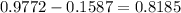
Multiplying by the number of bulbs, we have:
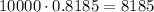
So the answer is 8185 bulbs.
6) The proportion was calculated above, it is 0.8185 = 81.85%