At the point of intersection, the value of y for the systems of equations is the same. Hence, we can relate the two equations as
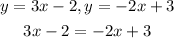
Solve for the value of x for the point of intersection, we have
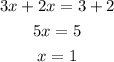
Use one of the equations on the systems of equations to solve for y. In this case, I will use y = 3x -2. Solve for y, we get
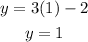
Hence, the point of intersection of the two equations is in (1,1) which is described by point D.