Inequalities and absolute value
We want to solve the following inequality for x:
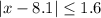
First, let's analyze the possibilities for the absolute value |x - 8.1|. We know that the absolute value is referred always to a positive quantity, then

We have two possible cases here:
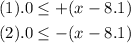
We are going to analyze the first case
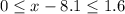
We add 8.1 on the three sides:
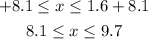
Now, we are going to analyze the second case
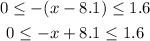
Substracting 8.1 on the three sides:

Now we multiply by -1 on the three sides ( since it is a negative number multiplication the inequality signs change their direction):
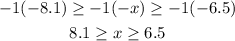
Then, we got two answers from both cases:
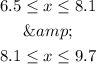
Combining them we have a final answer:
Answer: 6.5 ≤ x ≤ 9.7. The range of weights is from 6.5 pounds to 9.7 pounds