Question

13) f(x) = 2x4 + 3x3 + 6x2 + 12x - 8 A) f(x) = (2x - 1)(x + 2)(x + 2)(x - 2) C) f(x) = (2x + 1)(x - 2)(x + 2i)(x - 2i) B) f(x) = (2x - 1)(x + 2)(x + 2i)(x - 2i) D) f(x) = (2x + 1)(x - 2)(x + 2)(x - 2)

Answer 1

B. f(x) = (2x - 1)(x + 2)(x + 2i)(x - 2i)

Step-by-step explanation:

To find the answer, we need to calculate the product of every option and compare it with the initial function.

So, for A , we get:

`\begin{gathered} f(x)=\mleft(2x-1\mright)\mleft(x+2\mright)\mleft(x+2\mright)\mleft(x-2\mright) \\ f(x)=(2x^2+4x-x-2)(x+2)(x-2) \\ f(x)=(2x^2+3x-2)(x+2)(x-2) \\ f(x)=(2x^3+4x^2+3x^2+6x-2x-4)(x-2) \\ f(x)=(2x^3+7x^2+4x-4)(x-2) \\ f(x)=2x^4-4x^3+7x^3-14x^2+4x^2-8x-4x+8 \\ f(x)=2x^4+3x^3-10x^2-12x+8 \end{gathered}`

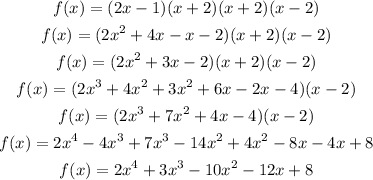
Therefore, option A is not the correct answer.

For C, we get:

`\begin{gathered} f(x)=\mleft(2x+1\mright)\mleft(x-2\mright)\mleft(x+2i\mright)\mleft(x-2i\mright) \\ f(x)=(2x^2-4x+x-2)(x+2i)(x-2i) \\ f(x)=(2x^2-3x-2)(x+2i)(x-2i) \\ f(x)=(2x^2-3x-2)(x^2-(2i)^2) \\ f(x)=(2x^2-3x-2)(x^2-4(-1)) \\ f(x)=(2x^2-3x-2)(x^2+4) \end{gathered}`
`\begin{gathered} f(x)=2x^4+8x^2-3x^3-12x-2x^2-8 \\ f(x)=2x^4-3x^3+6x^2-12x-8 \end{gathered}`

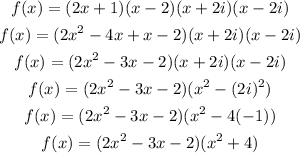
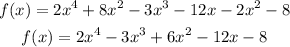
Therefore, option C is not the correct answer.

Finally, for B, we get:

`\begin{gathered} f(x)=\mleft(2x-1\mright)\mleft(x+2\mright)\mleft(x+2i\mright)\mleft(x-2i\mright) \\ f(x)=(2x^2+3x-2)(x^2+4) \\ f(x)=2x^4+8x^2+3x^3+12x-2x^2-8 \\ f(x)=2x^4+3x^3+6x^2+12x-8 \end{gathered}`

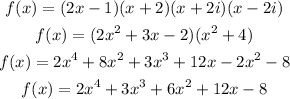
Therefore, the answer is B.