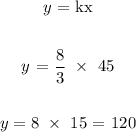The value of y when x = 45 is 120
Here, we have a direct variation question
Let us have the constant of variation as k
Since it is a direct variation, the relationship between the two is;
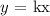
We can find the value of k from the initial values of x and y given
Mathematically, that would be;
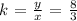
Now, we want to find the value of y when is 45
Recall;