Question

Algebraic Relation A = Tr2 A= Area r= radius e) What is the radius of a circle with area 25t?

Answer 1

Recalling the formula for the area of a circle:

`A=\pi\cdot r^2`

Divide both sides of the equation by the constant pi :

`(A)/(\pi)=r^2`

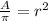
Take the square root of both sides of the equation and take the positive value of the square root, since r is a length and it is positive:

`\sqrt[]{(A)/(\pi)}=\sqrt[]{r^2}=r`

Therefore:

`r=\sqrt[]{(A)/(\pi)}`

Since A=25, then:

`r=\sqrt[]{(25)/(\pi)}=\frac{\sqrt[]{25}}{\sqrt[]{\pi}}=\frac{5}{\sqrt[]{\pi}}`

Use a calculator to find out the decimal representation of the number 5/sqrt(pi):

`r=\frac{5}{\sqrt[]{\pi}}\approx2.821`

Therefore, the radius of a circle with area 25 is approximately 2.821.