Question

the percentage of males and females in a certain country that hold a degree can be modeled by the functionsF(t)= 0.59t + 29.54M(t)= 0.42 + 30.22

Answer 1

The function that model the percentage of females in the country who hold a degree t years since 2010 is:

`F(t)=0.59t+29.54`

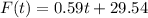
And the function that model the percentage of males in the country who hold a degree t years since 2010 is:

`M(t)=0.42t+30.22`

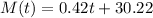
Now, to find the year at which the % of males and females who hold a degree are the same, then you need to find F(t)=M(t), replace the functions and find t as follows:

`\begin{gathered} F(t)=M(t) \\ 0.59t+29.54=0.42t+30.22 \\ \text{subtract 29.54 from both sides} \\ 0.59t+29.54-29.54=0.42t+30.22-29.54 \\ 0.59t=0.42t+0.68 \\ \text{Subtract 0.42t from both sides} \\ 0.59t-0.42t=0.42t-0.42t+0.68 \\ 0.17t=0.68 \\ \text{divide both sides by 0.17} \\ (0.17t)/(0.17)=(0.68)/(0.17) \\ \text{Simplify} \\ t=4 \end{gathered}`

Then, let's evaluate both functions at t=4 to check:

`\begin{gathered} F(4)=0.59*4+29.54=31.9 \\ M(4)=0.42*4+30.22=31.9 \end{gathered}`

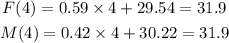
Thus, the year will be 2010+4=2014