Question

Find x, the angle of depression from the top of a lighthouse that is 157 ft above water level to the waterline of a ship 906 ftoff shore. Round your answer to the nearest tenth of a degree.

Answer 1

9.8°

Step-by-step explanation:

We can model the situation as follows:

So, we need to calculate the value of x.

The sides of the triangle and the angle x are related by the following trigonometric function:

`\begin{gathered} \tan x=\frac{Opposite\text{ side}}{Adjacent\text{ side}} \\ \tan x=(157)/(906) \end{gathered}`

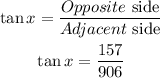
Therefore, we can solve for x, using the inverse function of tangent as follows:

`\begin{gathered} \tan x=0.17 \\ x=\tan ^(-1)(0.17) \\ x=9.8 \end{gathered}`

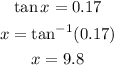
Then, the angle of depression is 9.8°