Given:
Number of new words to learn everyday = 2
Number of words he can spell already = 10
Let's write an inequality to determine the number of whole days it will take for him to be able to spell at least 75 words.
Apply the slope intercept form:
y = mx + b
Where m is the rate of change and b is the initial value.
We have the inequality:
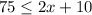
Where:
Initial value = 10
Rate of change = 2
Let's solve for x.
Subtract 10 from both sides:
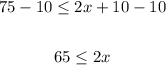
Divide both sides by 2:
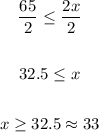
Therefore, it will take him aa minimum of 33 days to be able to spell at least 75 words.
ANSWER:
33 days