In order to x+5 to be a factor of the other polynomial, the zero of x+5 must also be a zero of the other polynomial.
The zero of x+5 is equal to x = -5.
So, using x = -5 in the other polynomial, we have:
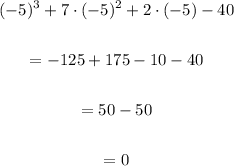
Since the result is zero, the value x = -5 is a zero of the second polynomial, therefore x+5 is a factor of the second polynomial.
Answer: Yes.