How do we do this system of equations?1. \: (3)/(x - 2y) + (2)/(2x + y) = 3(2)/(x - 2y) - (1)/(4x + 2y) = (1)/(6)

Question

How do we do this system of equations?
`1. \: (3)/(x - 2y) + (2)/(2x + y) = 3`
`(2)/(x - 2y) - (1)/(4x + 2y) = (1)/(6)`

Answer 1

Write out the equation given

`\begin{gathered} (3)/(x-2y)+(2)/(2x+y)=3\ldots\text{equation 1} \\ (2)/(x-2y)-(1)/(4x+2y)=(1)/(6)\ldots\text{equation 2} \end{gathered}`

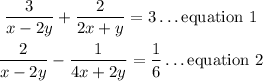
Rewrite the equation as

`\begin{gathered} \text{let} \\ x-2y=p \\ 2x+y=q \end{gathered}`

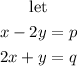
Then, the equation 1 becomes

`(3)/(p)+(2)/(q)=3`

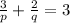
Then, equation 2 becomes

`\begin{gathered} (2)/(x-2y)-(1)/(4x+2y)=(1)/(6) \\ (2)/(x-2y)-(1)/(2(2x+y))=(1)/(6) \\ \text{Then} \\ (2)/(p)-(1)/(2q)=(1)/(6) \end{gathered}`

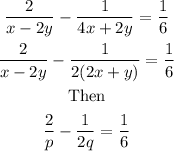
Then, the new equation becomes

`\begin{gathered} (3)/(p)+(2)/(q)=3 \\ \text{and } \\ (2)/(p)-(1)/(2q)=(1)/(6) \end{gathered}`

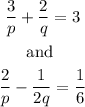
Then we solve the system of equation above

`\begin{gathered} (3)/(p)=3-(2)/(q) \\ \text{The}n \\ p=-(3q)/(2-3q) \end{gathered}`

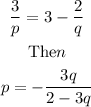
Then , substitute into the second equation, we have

`\begin{gathered} \begin{bmatrix}(2)/(-(3q)/(2-3q))-(1)/(2q)=(1)/(6)\end{bmatrix} \\ \text{Hence },\text{ simplify we have } \\ \begin{bmatrix}(12q-11)/(6q)=(1)/(6)\end{bmatrix} \end{gathered}`

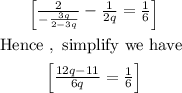
Then isolate q from the eequation above, we have

`\begin{gathered} (12q-11)/(6q)=(1)/(6) \\ 6q=6(12q-11) \\ 6q=72q-66 \\ 6q-72q=-66 \\ -66q=-66 \end{gathered}`

Hence

`q=-(66)/(-66)=1`

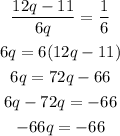
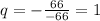
Hence q=1

Substitute to find the value of p, we have

`\begin{gathered} p=-(3q)/(2-3q) \\ p=-(3(1))/(2-3(1))=-(3)/(2-3)=-(3)/(-1)=3 \end{gathered}`

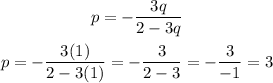
P = 3

Recall that

`\begin{gathered} p=x-2y \\ q=2x+y \\ \text{Then } \\ 3=x-2y \\ 1=2x+y \end{gathered}`

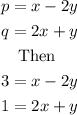
Hence

`\begin{gathered} x-2y=3\Rightarrow x=3+2y \\ 2(3+2y)+y=1\Rightarrow6+4y+y=1 \\ \text{Then } \\ 5y=1-6 \\ 5y=-5 \\ \text{Hence } \\ y=-1 \end{gathered}`

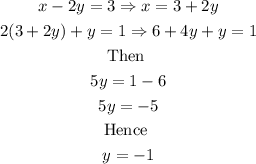
Thus,

`\begin{gathered} x=3+2y \\ x=3+2(-1)=3-2=1 \\ x=1 \end{gathered}`

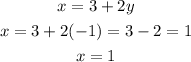
Therefore

x=1, y= -1