Question

$14,929 is invested part at 9% and the rest at 6% if the interest earned from the amount invested at 9% exceeds the interest earned from the amount invested at 6% by $1139.91 how much is invested at each rate Amount invested at 9%Amount invested at 6%

Answer 1

Let's call the amount invested at 9% as x, and the amount invested at 6% as y. The initial amount is $14,929, this means

`x+y=14929`

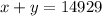
The amount invested at 9% exceeds the interest earned from the amount invested at 6% by $1139.91, which means

`1.09x=1.06y+1139.91`

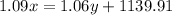
If we rewrite the first equation with x as a function o y, we can substitute our x value in the second equation and get an equation only for y.

`x=14929-y\Rightarrow1.09(14929-y)=1.06y+1139.91`

Solving for y:

`\begin{gathered} 1.09(14929-y)=1.06y+1139.91 \\ 16272.61-1.09y=1.06y+1139.91 \\ -2.15y=1139.91-16272.61 \\ -2.15y=-15133.61 \\ y=(-15133.61)/(-2.15)=7038.88837209\ldots\approx7038.89 \end{gathered}`

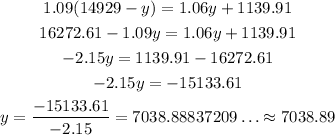
Using our first equation to find the value for x, we have

`\begin{gathered} x+7038.89=14929 \\ x=7890.11 \end{gathered}`

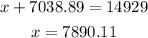
Amount invested at 9% = $7890.11

Amount invested at 6% = $7038.89