Question

A machine that manufactures automobile parts produces defective parts 12% of the time. If 8 parts produced by this machine are randomly selected, what is the probability that fewer than 3 of the parts are defective?Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.

Answer 1

The binomial distribution is

`\begin{gathered} P(X=k)=(nbinomialk)p^k(1-p)^(n-k) \\ n\rightarrow\text{ total number of trials} \\ k\rightarrow\text{ number of successful trials} \\ p\rightarrow\text{ probability of a successful trial} \end{gathered}`

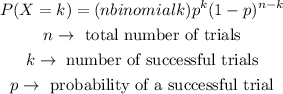
Therefore, in our case, the function is (Notice that 12%=0.12)

`\begin{gathered} \Rightarrow P(X=k)=(8binomialk)(0.12)^k(1-0.12)^(8-k) \\ \Rightarrow P(X=k)=(8binomialk)(0.12)^k(0.88)^(8-k) \end{gathered}`

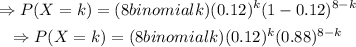
Thus, we need to find the probability that fewer than 3 of the 8 parts are defective; this is,

`P(X<3)=P(X=0)+P(X=1)+P(X=2)`

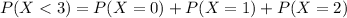
Calculating P(0), P(1), and P(2),

`\begin{gathered} P(X=0)=(8binomial0)(0.12)^0(0.88)^8=(8!)/((8-0)!0!)(1)(0.88)^8=0.88^8=0.35963452... \\ P(X=1)=(8!)/((8-1)!1!)(0.12)^1(0.88)^7=8(0.12)^1(0.88)^7=39.232857... \end{gathered}`

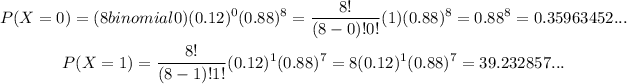
and

`P(X=2)=(8!)/(6!2!)(0.12)^2(0.88)^6=28(0.12)^2(0.88)^6=0.18724772...`

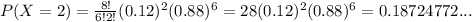
Hence,

`\Rightarrow P(X<3)\approx0.9392`

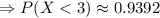
The rounded answer is 0.9392