Given:
price p = $25
number of x units = -8p + 400
Find: solve for the value of x
Solution:
To determine the value of x, simply replace the variable "p" in the equation with 25.
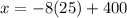
Then, solve.
Multiply -8 and 25.
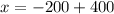
Add -200 and 400.
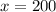
Therefore, at $25, 200 units were sold.
Part F:
Since the equation of the revenue is R(x) = -8p² + 400p, then the graph must be a parabola opening down. Out of the 4 options, Only Options A and D show this.
However, upon comparing the two options, we see that the y-axis of the two graphs is different. Option A says that the y-axis is the price p while Option D says that the y-axis is the revenue R.
Since the given function is the revenue, then the y-axis should be R. The correct graph is Graph D.
Part G:
If the revenue is at least $4032, then let's replace the r(x) function with 4, 032.
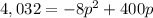
To solve for p, let's equate the function to zero by subtracting both sides of the function by 4, 032.

Then, let's solve for the value of "p" using the quadratic formula.
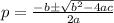
Note that in the revenue function above, a = -8, b = 400, and c = -4032. Let's plug these values into the formula above.
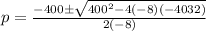
Then, simplify.

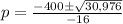
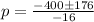
Separate the plus and minus operations.
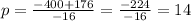

The values of p are 14 and 36.
Hence, the company should charge a price between a minimum of $14 and a maximum of $36 to have a revenue of at least $4,032.